learningnotes_js_algorithm

发表于 本文字数： 3.4k 阅读时长 ≈ 12 分钟

Javascript

2 算法与数据结构

（如果对算法不熟悉，可以在 LeetCode 上刷题，先从数组开始刷题，再到链表等，按这样的顺序刷题。）

2.1 数据结构：数组

数组不管在 C 这类结构化程序语言，还是 Java 等这类面向对象的程序语言，再到 Javascript 这种脚本语言，都是一种非常之基础的数据结构。

数组不管在 C 这类结构化程序语言，还是 Java 等这类面向对象的程序语言，再到 Javascript 这种脚本语言，都是一种非常之基础的数据结构。

数组不管在 C 这类结构化程序语言，还是 Java 等这类面向对象的程序语言，再到 Javascript 这种脚本语言，都是一种非常之基础的数据结构。

2.1.1 与数组有关的知识

0 数组，可以通过数组的下标索引的方式获取下标下面相对应的数据

=》 这种访问方式又叫随机访问

1 数组的索引（下标）都是从 0 开始。（下图以一字符数组为例，补充，数组内的数据都是由 0 开始，按顺序存储的）

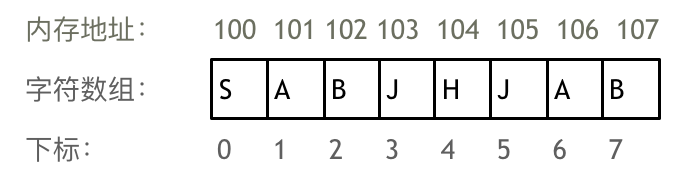
2 数组的内存空间地址 是连续的。正因为这种特性，对数组当中的数据进行增删操作的时候，就需要移动其他元素的内存地址。

3 数组中任意位置删除元素：数组当中的元素是不能直接删除的 （指地址和下标索引），只能通过对目标元素外元素的内存地址的修改进行数据的覆盖；例如，要想删除下标为 2 的元素，则要对下标为 2 后面的所有元素作移动操作 （指将元素对应的内存地址修改为前一位的内存地址，再将后面空出来的内存空间删除）。

3.5 补充，数组中任意位置插入元素：先在数组末尾分配内存空间；将目标位置以及后面位置的元素对应的内存地址及下标往后移动（指将元素对应的内存地址修改为后一位的内存地址）；最后将元素写入到目标位置中（写入元素之前的目标位置是空着的，但是内存地址和下标没有变）。

3.75 总结：数组的各项操作速度

访问 修改 添加 删除
快（随机访问） 快（随机访问） 慢（需要修改元素对应的内存地址） 慢（需要修改元素对应的内存地址）

时间复杂度：访问和修改操作为 O(1)，添加和删除操作 O(n)

4 数组通常使用关键字 array 来表示。

5 常见的数组除了简单的一维数组，还有更复杂的二维数组

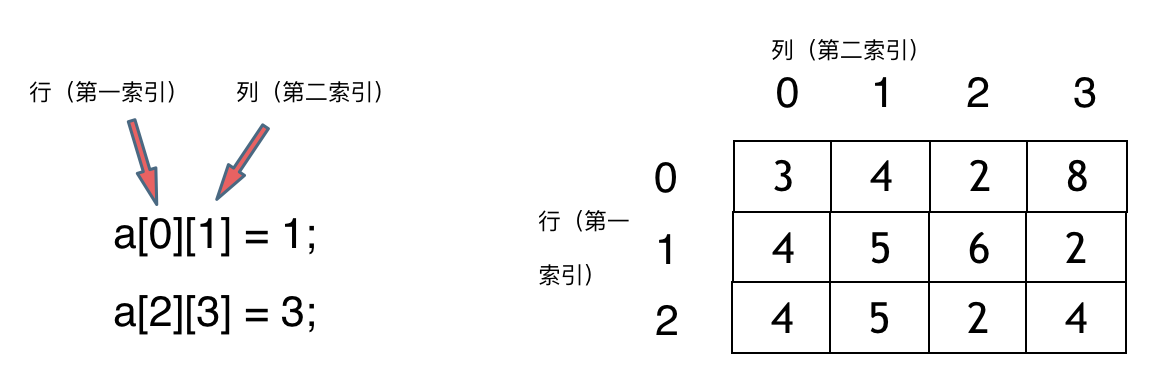
6 二维数组的内存空间地址分布也是连续的，一般都是从第一行第一个元素开始，到最后一个元素结束，接着到第二行的第一个元素，如此往复，可以发现数组上一行的最后一个元素与本行的第一个元素内存地址分布是连续的。

所以二维数组看起来是按面分布的，实际上还是线性分布的，因为二维数组的内存地址分布就是线性的。

《代码随想录》对数组内存地址的解释：

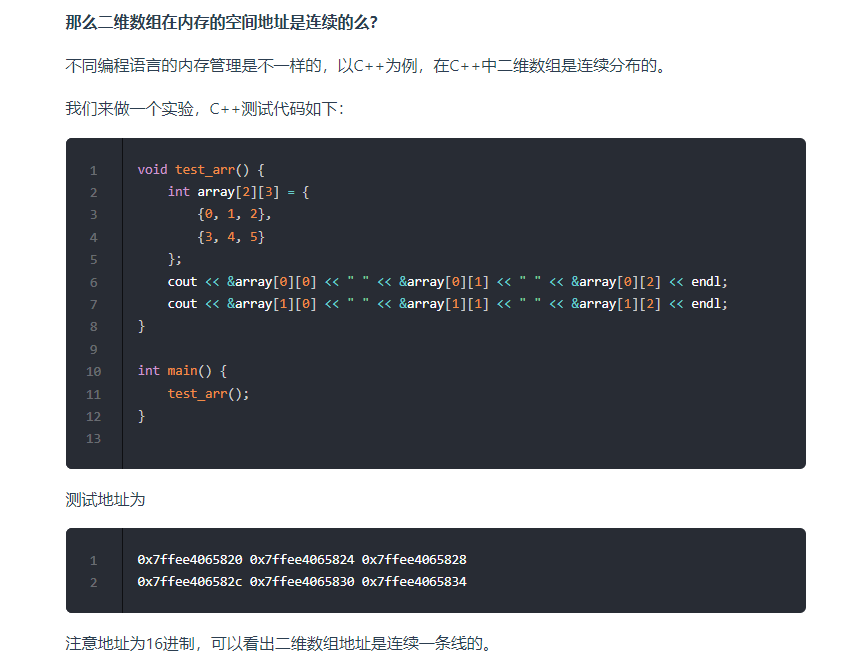
7 在 JavaScript 的数组中，可以存放各种类型的数据，其他语言的数组基本上只能存一种类型的数据 （有待考察）

8 没了

2.1.2 算法：二分查找

二分法，即一分为二的方法。

要求：数据为升序排序（非升序排序的数据要先排序）

基本法：设一序列 arr[]，序列中包含若干数据，且数据按升序排序，若之前已经给定了目标值 target，则先由序列的中间位置 middle 开始比较（middle 的值由左边界 left 和右边界 right 的和的平均值来决定；若 middle 值为非正整数，则将值向下取整后再 + 1，此时的 middle 中间值有两个。）

1 若当前位置（当前为中间位置 middle）arr[middle] 的值等于 target（arr[middle] === target，以下为方便之间简写），即查找成功

2 若当前位置（当前为中间位置 middle）arr[middle] 的值不等于 target（arr[middle] !== target，以下为方便之间简写），有以下两种情况

2.1 若 arr[middle] > target (target < arr[middle])，则在序列 arr[] 的前半段查找，即 [arr[left], arr[middle - 1]] （此时的左边界不变，右边界更改为 middle - 1，而不是 right）

2.2 若 arr[middle] < target** (target > arr[middle])，则在序列 arr[] 的后半段查找，即 [arr[middle + 1], arr[right]] （此时的右边界不变，左边界更改为 middle + 1，而不是 left**）

直到找到为止。

该算法的时间复杂度为 O(n)

以 LeetCode 704. 二分查找 为例：Question Link

（难度：简单）

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

解法如下 （只使用二分查找法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
function search(nums,target) {
    let left = 0;
    let right = nums.length - 1;

    while (left <= right) {
        let middle = Math.floor((left + right) / 2)
        if (nums[middle] > target) {
            right = middle - 1
        } else if (nums[middle] < target) {
            left = middle + 1
        } else {
            return middle
        }
    }

    return -1
}

console.log(search([-1,0,3,5,9,12],9))
console.log(search([-1,0,3,5,9,12],2))

输出结果如下

1
2
4  -》 console.log(search([-1,0,3,5,9,12],9))
-1 -》 console.log(search([-1,0,3,5,9,12],2))

举一反 n

LeetCode 35. 搜索插入位置：Question Link

（难度：简单）

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

1
2
输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

1
2
输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

1
2
输入: nums = [1,3,5,6], target = 7
输出: 4

解法如下 （只使用二分查找法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const searchInsert = function(nums, target) {
    let left = 0;
    // let index = nums.length;
    let right = nums.length - 1;


    while (left <= right) {
        let middle = Math.floor((left + right) / 2)
        if (nums[middle] > target) {
            right = middle - 1
        } else if (nums[middle] < target) {
            left = middle + 1
        } else {
            return middle
        }
    }
    return right + 1
};

console.log(searchInsert([1,3,5,6],5))
console.log(searchInsert([1,3,5,6],2))
console.log(searchInsert([1,3,5,6],7))

输出结果

1
2
3
2 -》 console.log(searchInsert([1,3,5,6],5))
1 -》 console.log(searchInsert([1,3,5,6],2))
4 -》 console.log(searchInsert([1,3,5,6],7))

举一反 n

LeetCode 69. x 的平方根：Question Link

（难度：简单）

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5

示例 1：

1
2
输入：x = 4
输出：2

示例 2：

1
2
3
输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

解法如下 （只使用二分查找法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const mySqrt = function (x) {
    if (x === 1) {
        return 1
    }
    let left = 0;
    let right = x;

    while (left <= right) {
        let middle = left + Math.floor((right - left) / 2)
        if (x === middle * middle) {
            return middle
        }
        if (x > middle * middle) {
            left = middle + 1
        } else {
            right = middle - 1
        }
    }

    return right
};

console.log(mySqrt(4))
console.log(mySqrt(8))

输出结果

1
2
2 -> console.log(mySqrt(4))
2 -> console.log(mySqrt(8))

举一反 n

LeetCode 367. 有效的完全平方数：Question Link

（难度：简单）

给定一个 正整数 num ，编写一个函数，如果 num 是一个完全平方数，则返回 true ，否则返回 false .

进阶：不要 使用任何内置的库函数，如 sqrt .

示例 1：

1
2
输入：num = 16
输出：true

示例 2：

1
2
输入：num = 14
输出：false

解法如下（只使用二分查找法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const isPerfectSquare = function(num) {
    if (num === 1) {
        return true
    }

    let left = 0;
    let right = num;

    while (left <= right) {
        let middle = left + Math.floor((right - left) / 2)

        if (num === middle * middle) {
            return true
        }
        if (num > middle * middle) {
            left = middle + 1
        } else if (num < middle * middle) {
            right = middle - 1
        } else {
            return true
        }
    }
    return false
};

console.log(isPerfectSquare(16))
console.log(isPerfectSquare(14))

执行结果

1
2
true  -> console.log(isPerfectSquare(16))
false -> console.log(isPerfectSquare(14))

举一反 n

LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置：Question Link

（难度：中等）

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1
2
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

1
2
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

1
2
输入：nums = [], target = 0
输出：[-1,-1]

这道题目，建议写两个二分函数，查找左边界一个以及查找右边界一个

解法如下 （只使用二分查找法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
const findLeftBorder = function (nums, target) { // 查找左边界
    let left = 0;
    let right = nums.length - 1;
    let leftBorder = -2;

    while (left <= right) {
        let middle = Math.floor((left + right) / 2)
        if (nums[middle] >= target) {
            right = middle - 1
            leftBorder = right
        } else {
            left = middle + 1

        }
    }
    return leftBorder
}

const findRightBorder = function (nums, target) { // 查找右边界
    let left = 0;
    let right = nums.length - 1;
    let rightBorder = -2;

    while (left <= right) {
        let middle = Math.floor((left + right) / 2)
        if (nums[middle] > target) {
            right = middle - 1
        } else {
            left = middle + 1
            rightBorder = left

        }
    }
    return rightBorder
}


const searchRange = function(nums, target) { // 用上面获取到的边界位置来获取边界元素

    let leftBorder = findLeftBorder(nums, target)
    let rightBorder = findRightBorder(nums, target)

    if (leftBorder === -2 || rightBorder === -2) {
        return [-1, -1]
    } else if (rightBorder - leftBorder > 1) {
        return [leftBorder + 1, rightBorder - 1]
    } else {
        return [-1, -1]
    }

};

console.log(searchRange([5,7,7,8,8,10],8))
console.log(searchRange([5,7,7,8,8,10],6))
console.log(searchRange([],0))

输出结果如下

1
2
3
[ 3, 4 ]   -》 console.log(searchRange([5,7,7,8,8,10],8))
[ -1, -1 ] -》 console.log(searchRange([5,7,7,8,8,10],6))
[ -1, -1 ] -》 console.log(searchRange([],0))

2.1.3 算法：双指针

2.1.3.1 双指针
2.1.3.2 滑动窗口

2.1.4 （番外）算法？对过程的模拟！

2.1.5 算法：做好初始定义

2.1.6 数组中基本的算法思想

2.1.7 算法：对撞指针

2.2 数据结构：链表

链表与数组一样都是非常之基础的一种数据结构

链表与数组一样都是非常之基础的一种数据结构

链表与数组一样都是非常之基础的一种数据结构

2.2.1 与链表有关的知识

2.2.1.1 单链表

一个基本的链表结构就是 单链表

基本结构：

可以看到，链表是一种通过 指针 相串联的一种线性数据结构。

每一个节点由两部分组成：数据区域（Data） 和 指针区域（Pointer），数据区域用来存数据，指针区域用来存放指向下一个区域的指针（一般叫做 next）

一个链表的入口节点，叫做链表的头节点，也就是 head

最后一个节点的指针指向 空指针（null）

单链表只能向后查询。

单链表只能向后查询。

单链表只能向后查询。

2.2.1.2 双链表

如图

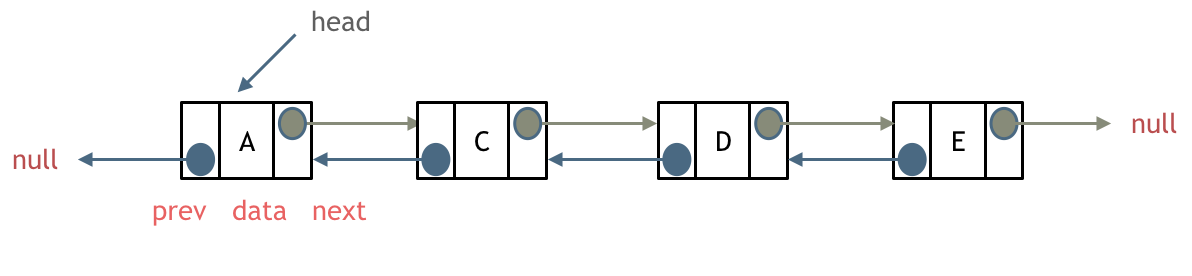
双链表除了拥有上面单链表的结构外，每个节点还有额外的一个指针区域，用来存放指向上一个区域的指针（一般叫做 prev）

这样双链表就可以向前查询和向后查询，实现双向查询。

2.2.1.3 循环链表

顾名思义，循环链表就是将链表的首尾连在一起，这里不详细叙述，也不放图了。

2.2.1.4 与数组有关的知识

1 我们知道，数组在内存空间当中是连续分布的。但链表可不是这样分布的。链表是通过指针区域内的指针链接到内存中的各个节点，所以链表当中的节点在内存空间中是散乱分布的，具体怎么分配由操作系统的内存管理机制来定

2 与数组不同，链表节点需要预先定义：（以 JavaScript 为例）

1
2
3
4
5
6
class ListNode() {
    constructor(val,next){
        this.val = val
        this.next = next
    }
}

3 链表的操作包括：添加节点和删除节点。

3.33 添加节点：要想在目标位置添加链表节点，首先先新建节点；然后把目标位置的上一个节点指针指向这个新节点（指针指向的内存地址指向（修改为）新节点的内存地址）；最后新节点的指针指向目标位置的下一个节点 （指针指向的内存地址指向（修改为）原下一个节点的内存地址）

3.66 删除节点：要想在目标位置删除链表节点，只需将目标节点的上一个节点的指针指向目标节点的下一个节点即可（指针指向的内存地址指向（修改为）目标节点的下一个节点的内存地址）。对于 C++、C 这类语言还需要手动释放这个目标节点，而 Java、Python、JavaScript 有内存回收机制，不用手动释放。

3.75 删除的特例：若删除尾节点，要从头节点查找到倒数第二个节点，将倒数第二个节点通过 next 指针指向 null，查找所需的时间复杂度为 O(n)

3.99 总结：链表的各项操作速度

访问 修改（元素数据） 添加 删除
慢 慢 快 快

所需时间复杂度：访问 O(n)，增删 O(1)

2.2.2 算法：虚拟头节点

2.2.3 算法：双指针

2.2.4 算法：虚拟头节点与双指针的巧妙运用

2.3 数据结构：哈希表（HashTable）

2.9

2.10