代码随想录刷题记录 Day2

发表于 更新于 本文字数： 2.6k 阅读时长 ≈ 9 分钟

To Do List

  • DAY 1 回顾
  • LeetCode 977. 有序数组的平方 / Squares of a Sorted Array
  • 滑动窗口基础
  • LeetCode 209. 长度最小的子数组 / Minimum Size Subarray Sum
  • 209 题扩展题目
  • 再提循环不变量：LeetCode 59. 螺旋矩阵 II / Spiral Matrix II
  • 59 题扩展题目
  • 总结 / Summary

1. DAY 1 回顾

Day 1 学习内容：Link

  • 认识了数组的基本结构和增删查改操作。
  • 学习了二分法以及双指针法
  • 一刷 LeetCode 6 题 Link

2. LeetCode 977. 有序数组的平方 / Squares of a Sorted Array

难度：简单

题目要求：

（CN）

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

  • 请你设计时间复杂度为 O(n) 的算法解决本问题

（EN）

Given an integer array nums sorted in non-decreasing order, return an array of the squares of each number sorted in non-decreasing order.

Squaring each element and sorting the new array is very trivial, could you find an O(n) solution using a different approach?

Example 1:

1
2
3
4
5
6
7
8
9
Input: nums = [-4,-1,0,3,10]
Output: [0,1,9,16,100]
Explanation: After squaring, the array becomes [16,1,0,9,100].
After sorting, it becomes [0,1,9,16,100].

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

Example 2:

1
2
3
4
5
Input: nums = [-7,-3,2,3,11]
Output: [4,9,9,49,121]

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

Constraints / 提示:

  • 1 <= nums.length <= 10^4
  • -10^4 <= nums[i] <= 10^4
  • nums is sorted in non-decreasing order. (nums 已按 非递减顺序 排序)

与之前的数组不同的是，这道题当中数组包含了负数，而负数的平方为正数，要想平方后排序，需要用到两个快指针 fs 和 fe，分别指向数组的 0 位置和 nums.size - 1 位置 ，慢指针 s 则指向一个新数组的 nums.size - 1 位置，从右向左移动指针，记录平方后的元素；快指针则需要对平方后的元素进行比较：

1
2
1 若 (nums[fs])^2 > (nums[fe])^2，则将 nums[fs] 赋给 s，fs 向右移动一位，s 向左移动一位
2 否则将 nums[fe] 赋给 s，fe 向左移动一位，s 向左移动一位。

解法：

Java：

（For Leetcode / IDEA Custom）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {

    public static int[] sortedSquares(int[] nums) {
        int s = nums.length - 1;
        int[] square = new int[nums.length];
        for (int fs = 0, fe = nums.length - 1; fs <= fe;) {
            if ((nums[fs]*nums[fs]) > (nums[fe]*nums[fe])) {
                square[s--] = nums[fs]*nums[fs];
                fs++;
            } else {
                square[s--] = nums[fe]*nums[fe];
                fe--;
            }
        }
        return square;
    }

    public static void main(String[] args) {
        System.out.println(sortedSquares(new int[]{-4,-1,0,3,10}));
        System.out.println(sortedSquares(new int[]{-7,-3,2,3,11}));
    }
}

JavaScript：

（For Leetcode / WebStorm Custom）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @param {number[]} nums
 * @param {number} val
 * @return {number}
 */
/**
 * @param {number[]} nums
 * @return {number[]}
 */
var sortedSquares = function(nums) {
    let s = nums.length - 1
    let square = new Array(nums.length - 1).fill(-1)
    for (let fs = 0, fe = nums.length - 1; fs <= fe;) {
        if ((nums[fs]*nums[fs]) > (nums[fe]*nums[fe])) {
            square[s--] = nums[fs]*nums[fs];
            fs++
        } else {
            square[s--] = nums[fe]*nums[fe];
            fe--;
        }
    }
    return square
};

console.log(sortedSquares([-4,-1,0,3,10]))
console.log(sortedSquares([-7,-3,2,3,11]))

3. 滑动窗口基础

4. LeetCode 209. 长度最小的子数组 / Minimum Size Subarray Sum

难度：中等

题目要求：

（CN）

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [nums(l), nums(l+1), …, nums(r-1), nums(r)] ，并返回其长度。如果不存在符合条件的子数组，返回 0.

  • 如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

（EN）

Given an array of positive integers nums and a positive integer target, return the minimal length of a subarray whose sum is greater than or equal to target. If there is no such subarray, return 0 instead.

If you have figured out the O(n) solution, try coding another solution of which the time complexity is O(n log(n)).

Example 1:

1
2
3
4
5
6
7
Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

Example 2:

1
2
3
4
5
Input: target = 4, nums = [1,4,4]
Output: 1

输入：target = 4, nums = [1,4,4]
输出：1

Example 3:

1
2
3
4
5
Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

Constraints / 提示:

  • 1 <= target <= 10^9
  • 1 <= nums.length <= 10^5
  • 1 <= nums[i] <= 10^4

解法：

5. 209 题扩展题目

6. 再提循环不变量：LeetCode 59. 螺旋矩阵 II / Spiral Matrix II

难度：中等

题目要求：

（CN）

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

（EN）

Given a positive integer n, generate an n x n matrix filled with elements from 1 to n2 in spiral order.

Example 1:

img

1
2
3
4
5
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

Example 2:

1
2
3
4
5
Input: n = 1
Output: [[1]]

输入：n = 1
输出：[[1]]

Constraints / 提示:

  • 1 <= n <= 20

这道题本质上不涉及任何算法的，它主要考的就是一个过程的模拟。在二分法中，区间那块除了提到了左闭右闭区间，还提到了左闭右开区间，左闭右开区间针对多个连续的区间，最主要遵循的规则就是循环不变量规则，这回再把这个概念提出来，在解这道题的时候，也应把循环不变量用在过程模拟上面。

这循环不变量当中的 “量”，最主要指的就是判定规则作为循环遍历要保持一致，如果第一个区间规则是左闭右开 [l,r) ，那么后面的区间规则也应该是左闭右开，循环的规则要保持一致！

比如说这题，可以把正方形矩阵的四个角作为一个节点，如下图：

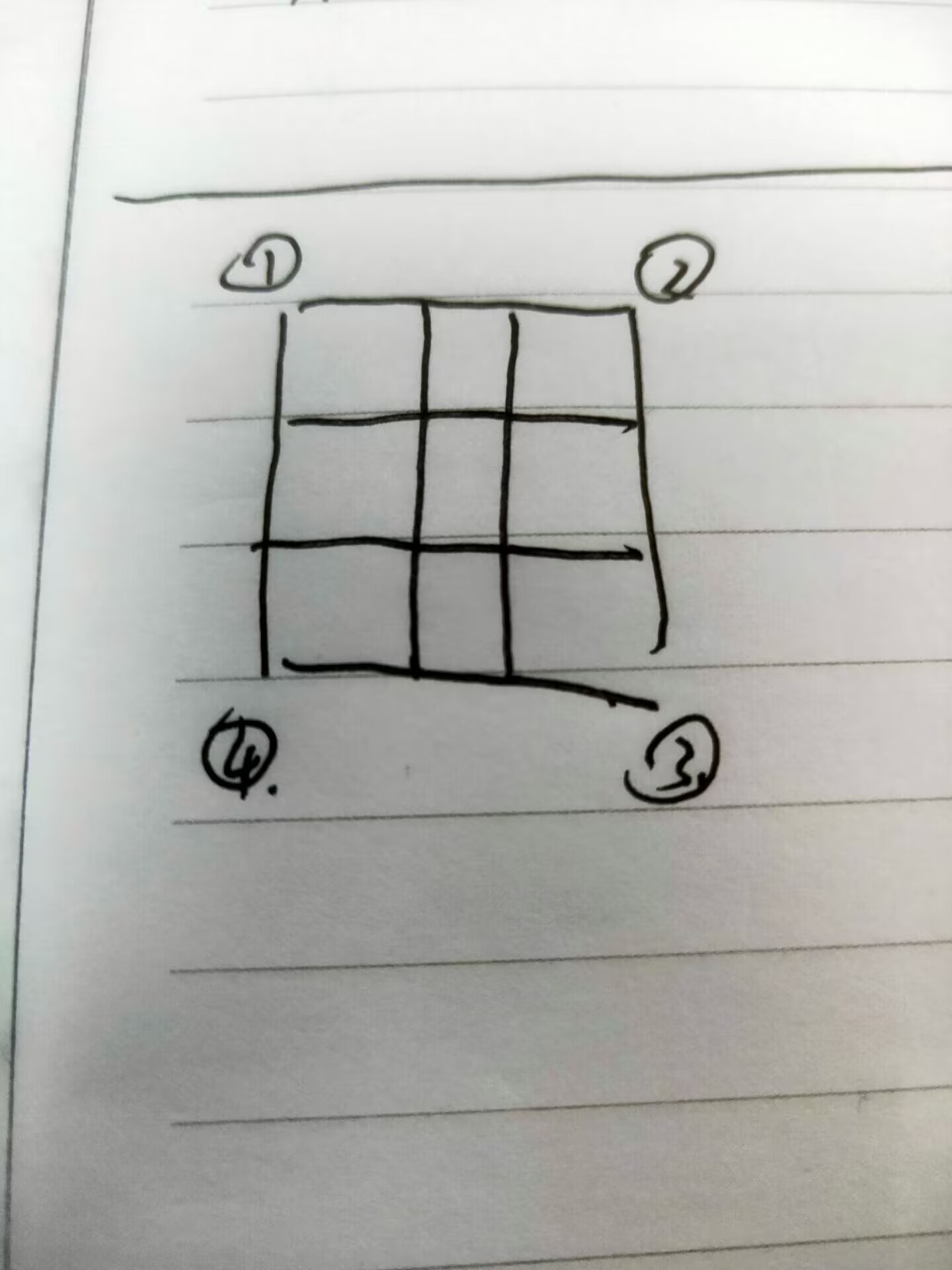
QQ图片20230218155538

在循环遍历一圈时，如果区间是左闭右开，那么后面循环的区间也要左闭右开，也就是

1
2
3
4
[1,2)
[2,3)
[3,4)
[4,1)

这样我们保持一个区间，这样正方形矩阵的所有节点都能采到了。

这里有个非常容易搞错的点，就是在数学坐标轴中，向右则横坐标 x 递增；而在数组 [i][j] 中，顺时针遍历数组，却是 j 递增（在数组 [i][j] 中，i 实际上是数组的行，j 实际上是数组的列）。这是因为数组顺时针遍历时，会先遍历数组的列，行并没有发生变化。根据上述结论，设初始行位置为 starty ，初始列位置为 startx ，初始的遍历方向为顺时针方向，再定义一个初始位置为[starty][startx] , 这里以矩阵节点 1 所在的位置为原点为例，那么节点 1 的 startx = 0, starty = 0. 接着就可以得出：

从节点 1 遍历到节点 2 时，数组向右遍历，列发生变化，即 j++；又因为区间是左闭右开，在遍历时不应采上下一个节点。题目中的变量 n 其实就是 n.length （假设变量 n = 3, 数组的索引位置为 0,1,2，则在数组y中的最后一个位置就是 n.length - 1），那么再引入一个新变量叫 offset ，用来控制遍历时不会采到下一个节点。综上所述第一个（横向）遍历区间应该为：

1
[starty, n.length-offset)

也就是

1
for (j = starty; j < n-offset; j++){}

第二个遍历区间，只需把 starty 换成 startx 即可，同时要注意数组顺时针遍历时的行列变化。即：

1
2
[startx, n.length-offset) -> 
for (i = startx; i < n-offset; i++){}

接着第三个区间、第四个区间，同样要注意数组顺时针遍历时的行列变化，即

1
2
3
4
5
[n.length-offset, starty)->
for (j = n-offset; j > starty; j--) {}

[n.length-offset, startx)->
for (i = n-offset, i > startx; i--) {}

这时一圈的遍历就算结束了。接下来，要继续往里遍历，则初始位置和偏移值都要发生递增变化：

1
2
3
startX++
startY++
offset++

这里又要分两种情况：

(1) 如果变量 n 为奇数，则不管转矩阵多少圈，最终都还剩中间一个没有遍历。所以应加一个判断

1
if(奇数) -> 矩阵最中间的值计入计数，计数+1

(2) 如果变量 n 为偶数，则重复上述的遍历过程。

至此，矩阵的遍历就算全部结束了。重点还是要多多理解矩阵遍历的过程！

解法：

JavaScript：

（For Leetcode / WebStorm Custom）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * @param {number} n
 * @return {number[][]}
 */

var generateMatrix = function(n) {
// function generateMatrix(n) {
    const res = new Array(n)
    for (let i = 0; i < n; i++) {
        res[i] = new Array(n)
    }
    let startx = 0, starty = 0;
    let loop = mid = Math.floor(n/2);
    let count = 1, offset = 1;
    while(loop--){
        i = startx;
        j = starty;
        for (j = starty; j < n - offset; j++) {
            res[startx][j] = count++
        }
        for (i = startx; i < n - offset; i++) {
            res[i][j] = count++
        }
        for (j = n-offset; j > starty; j--) {
            res[i][j] = count++
        }
        for (i = n-offset; i > startx; i--) {
            res[i][j] = count++
        }
        startx++
        starty++

        offset++
        
    }

    if (n % 2) {
        res[mid][mid] = count
    }

    return res
    // console.log(matrix)

};


7. 59 题扩展题目

LeetCode 54. 螺旋矩阵 / Spiral Matrix

难度：中等

要求：

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

(Given an m x n matrix, return all elements of the matrix in spiral order.)

Example 1:

spiral1

1
2
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

spiral2

1
2
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

和 59 题不一样的是，这题输出的结果是遍历后的新数组，所以需要新创建一个数组用来存储遍历结果；数组不是单由变量 n 来创建的，而是由涉及行的变量 n 和涉及列的变量 m 来共同创建的。多了一个变量的影响，遍历圈数应该是由最大值的变量来决定而不是最小值的变量：（如图）

由于矩阵现在变为长方形，不加跳出条件很容易造成新数组的长度大于原数组的长度，所以在存储代码块处添加跳出条件，若存储的长度与原数组的长度完全相等时，直接返回新数组。

解法：

还是类似于模拟过程的解法。

JavaScript：

（For Leetcode / WebStorm Custom）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
    let starty = 0, startx = 0
    let m = matrix.length
    let n = matrix[0].length
    let loop = matrix[0].length > matrix.length ? Math.floor(matrix[0].length / 2) : Math.floor(matrix.length / 2)
    let offset = 1
    let newArray = []
    if (matrix.length === 1) {
        for (j = 0; j < matrix[0].length; j++) {
            newArray.push(matrix[0][j])
        }
    } else if (matrix[0].length === 1) {
        for (i = 0; i < matrix.length; i++) {
            newArray.push(matrix[i][0])
        }
    } else {
        while (loop--) {
            let i = startx
            let j = starty
            for (j = starty; j < n - offset; j++) {
                newArray.push(matrix[startx][j])
                if(newArray.length === m*n) {
                    return newArray
                }
            }
            for (i = startx; i < m - offset; i++) {
                newArray.push(matrix[i][j])
                if(newArray.length === m*n) {
                    return newArray
                }
            }
            for (j = n - offset; j > starty; j--) {
                newArray.push(matrix[i][j])
                if(newArray.length === m*n) {
                    return newArray
                }
            }
            for (i = m - offset; i > startx; i--) {
                newArray.push(matrix[i][j])
                if(newArray.length === m*n) {
                    return newArray
                }
            }
            startx++
            starty++
            offset++
        }
        if (m % 2 && n % 2) {
            newArray.push(matrix[Math.floor(m/2)][Math.floor(n/2)])
        }
    }
    return newArray
};

8. 总结 / Summary